已知函数$f(x)=x(e^{\sin x}-\ln{}{x})-1$，试研究$g(x)=f(x)+1$的零点个数

解答

$$g(x)=f(x)+1=x(e^{\sin x}-\ln{}{x})$$由于$x>0$，可令$h(x)=e^{\sin x}-\ln{}{x}$，此时$h(x)$与$g(x)$有相同的零点。
$h(x)$的导数$$h'(x)=\cos xe^{\sin x}-\frac{1}{x}=\frac{x\cos xe^{\sin x}-1}{x}$$
①$x\in (0,\frac{\pi}{2})$时，$$h(x)>1-\ln{}{x}>1-\ln{}{\frac{\pi}{2}}>0$$故无零点
②$x\in (\frac{\pi}{2},\frac{3\pi}{2})$时，我们有$$h'(x)<h'(x)+\frac{1}{x}=\cos xe^{\sin x}<0$$恒成立，而$$h(\frac{\pi}{2})=e-\ln{}{\frac{\pi}{2}}>0,h(\frac{3\pi}{2})=\frac{1}{e}-\ln{}{\frac{3\pi}{2}}<0$$由零点存在性定理，$g(x)$在$x\in (\frac{\pi}{2},\frac{3\pi}{2})$内有一个零点。
③$x\in (\frac{3\pi}{2},\frac{5\pi}{2})$时，$$h''(x)=(1-\sin^2x-\sin x)e^{\sin x}+\frac{1}{x^2}$$$$h'''(x)=(-3\sin x\cos x-\sin^2x\cos x)e^{\sin x}-\frac{2}{x^3}<0$$故$h''(x)$在$(\frac{3\pi}{2},\frac{5\pi}{2})$上单调递减。
由于$$h''(\frac{3\pi}{2})>0,h''(\frac{5\pi}{2})<0$$故$h'(x)$在$(\frac{3\pi}{2},\frac{5\pi}{2})$上先增后减
而$$h'(\frac{3\pi}{2})<0,h'(2\pi)>0,h'(\frac{5\pi}{2})<0$$所以$h(x)$在$(\frac{3\pi}{2},\frac{5\pi}{2})$上先减后增再减
又$$h(\frac{3\pi}{2})=\frac{1}{e}-\ln{}{\frac{3\pi}{2}}<0,h(\frac{5\pi}{2})=e-\ln{}{\frac{5\pi}{2}}>0$$故我们可以找到$x_1,x_2\in (\frac{3\pi}{2},\frac{5\pi}{2})$
使$h(x_1)=h(\frac{3\pi}{2})<0,h(x_2)=h(\frac{5\pi}{2})>0$，且$h(x)$在$(x_1,x_2)$上单增。
由零点存在性定理，$g(x)$在$(x_1,x_2)$内有一个零点。
显然，$g(x)$在$(\frac{3\pi}{2},x_1)$和$(x_2,\frac{5\pi}{2})$上无零点。
故$g(x)$在$x\in (\frac{3\pi}{2},\frac{5\pi}{2})$内有一个零点。
④$x\in (\frac{5\pi}{2},\frac{7\pi}{2})$时，步骤同②，有一个零点
⑤$x\in (\frac{7\pi}{2},\frac{9\pi}{2})$时，步骤同③，有一个零点
⑥$x\in (\frac{9\pi}{2},\frac{11\pi}{2})$时，步骤同②，有一个零点
⑦$x\in (\frac{11\pi}{2},+\infty)$时，$$h(x)=e^{\sin x}-\ln{}{x}<e-\ln{}{x}<e-\ln{}{\frac{11}{2}\pi}<0$$故无零点。

综上，$g(x)$的零点个数为5个。

第一问其实类似于经典问题：求$\sin x$与$x$的交点个数，最直观的解决办法是画图找关键点。
第一问的函数求导后形式稍显复杂，再加上作为大题出现就显得十分繁琐。
$e^{\sin x}$(绿色)和$\ln{}{x}$(蓝色)的图像如下，画图工具为在线的Geogebra计算器。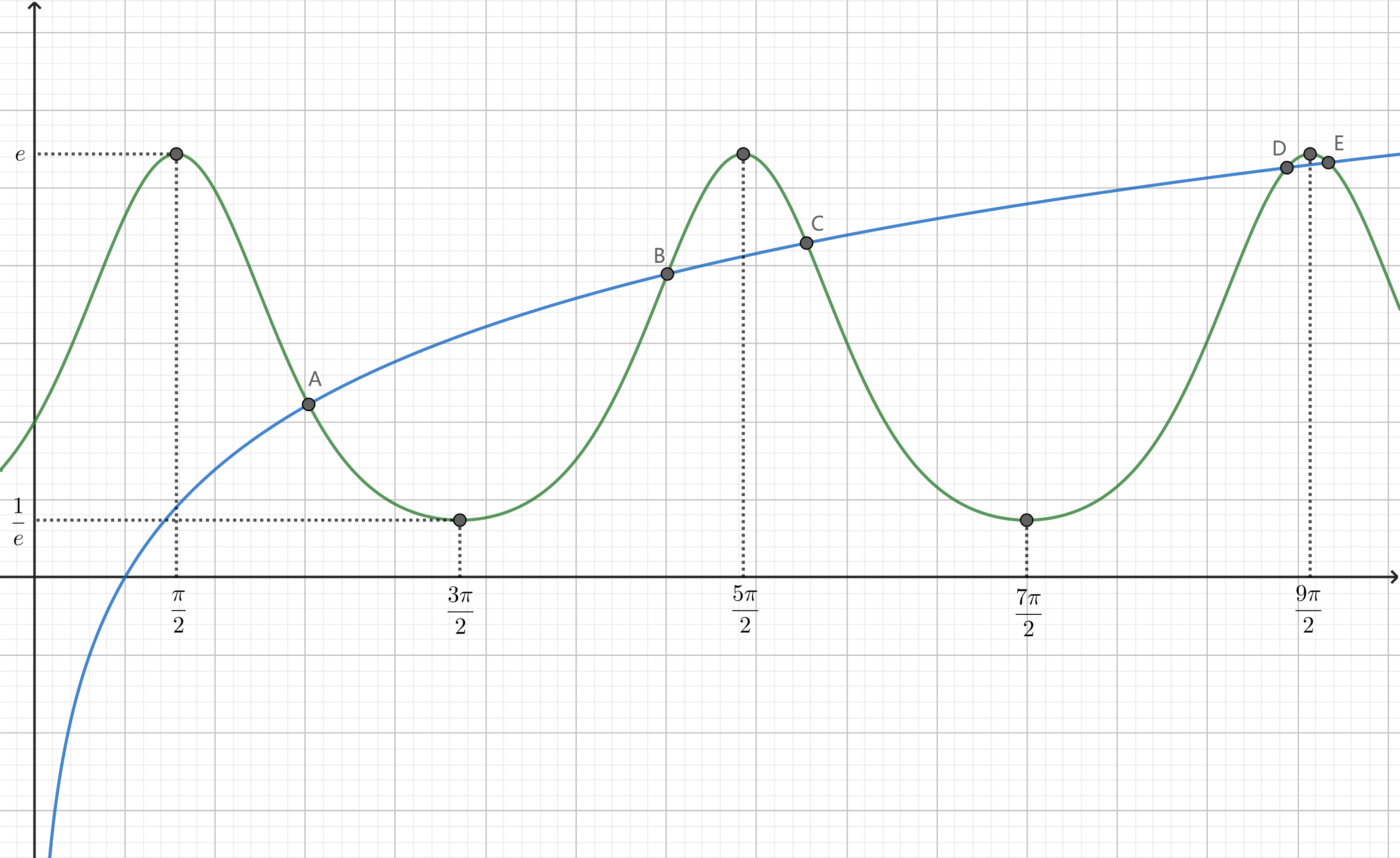

可以看到有五个交点。

本题第二问是：
设$f(x)$从左向右的4个零点依次为$x_1,x_2,x_3,x_4$。试证明：$$\frac{(x_2-x_1)^4+(x_4-x_3)^4+\ln{}{\frac{1}{3}}}{(x_4-x_1)^2-(x_3-x_2)^2}<\frac{3}{4}$$
有点零点偏移问题的感觉，但也有钓鱼嫌疑，暂无思路。